Прямая как линия пересечения двух плоскостей
Пусть относительно ПДСК заданы две плоскости своими общими уравнениями, пересекающихся по некоторой прямой: α: A1x+B1y+C1z+D1=0. β: A2x+B2y+C2z+D2=0. Запишем канонические уравнения прямой, полученные в результате пересечения плоскостей α и β. Пусть x0, y0, z0 - какое-либо решение
{A1x+B1y+C1z+D1=0.
{A2x+B2y+C2z+D2=0.
Точка M0(x0, y0, z0) принадлежит прямой пересечения плоскостей α и β. Покажем, что в качестве направляющего вектора прямой можно взять вектор a с координатами
{B1 C1 C1 A1 A1 B1}
{B2 C2,C2 A2,A2 B2}.
В самом деле, в силу необходимого и достаточного условия компланарности вектора и плоскости имеем N1={A1, B1, C1}, N2={A2, B2, C2}.
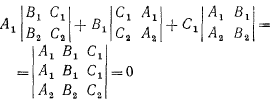
Так как определитель содержит две одинаковые строки, то направляющий вектор прямой, полученный в результате пересечения плоскостей α и β, компланарен плоскости α, а значит, и сама прямая компланарна плоскости α. Аналогично проверяем компланарность направляющего вектора прямой и плоскости β.
Таким образом, вектор а можно выбрать в качестве направляющего вектора прямой, полученной в результате пересечения плоскостей α и β. Каноническое уравнение прямой имеет вид: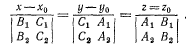
{A1x+B1y+C1z+D1=0.
{A2x+B2y+C2z+D2=0.
Точка M0(x0, y0, z0) принадлежит прямой пересечения плоскостей α и β. Покажем, что в качестве направляющего вектора прямой можно взять вектор a с координатами
{B1 C1 C1 A1 A1 B1}
{B2 C2,C2 A2,A2 B2}.
В самом деле, в силу необходимого и достаточного условия компланарности вектора и плоскости имеем N1={A1, B1, C1}, N2={A2, B2, C2}.
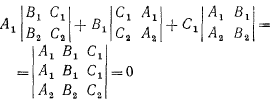
Так как определитель содержит две одинаковые строки, то направляющий вектор прямой, полученный в результате пересечения плоскостей α и β, компланарен плоскости α, а значит, и сама прямая компланарна плоскости α. Аналогично проверяем компланарность направляющего вектора прямой и плоскости β.
Таким образом, вектор а можно выбрать в качестве направляющего вектора прямой, полученной в результате пересечения плоскостей α и β. Каноническое уравнение прямой имеет вид:
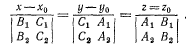
Всё для учебы » Аналитическая геометрия » Прямая как линия пересечения двух плоскостей