Двуполостный гиперболоид

Двуполостным гиперболоидом называется поверхность, заданная относительно специально выбранной системы координат уравнением x²/a²+y²/b²-z²/c²=-1 (1). Если точка (x, y, z) принадлежит двуполостному гиперболоиду (1), то на этой поверхности лежит точка с координатами (±x, ±y, ±z) при любом наборе знаков, следовательно начало координат является центром двуполостного гиперболоида, координатные оси — осями симметрии, координатные плоскости — плоскостями симметрии. Вершинами двуполостного гиперболоида называются точки пересечения поверхности с осью oz (0, 0, ±c).

http://uchim.org/algebra-i-geometrija/dvupolostnyj-giperboloid - uchim.org

Пусть в (1) a=b, тогда двуполостный гиперболоид получается вращением гиперболы x²/a²-z²/c²=-1 или z²/c²-x²/a²=1, у которой ось oz является её вещественной осью, а ox мнимой. Вращение гиперболы осуществляется вокруг оси oz. В этом случае двуполостный гиперболоид называется двуполостным гиперболоидом вращения.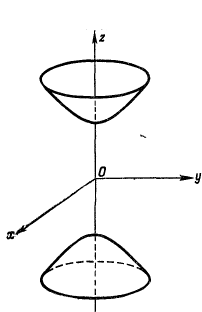

Всё для учебы » Аналитическая геометрия » Двуполостный гиперболоид