Однополостный гиперболоид

Однополостным гиперболоидом называется поверхность, заданная относительно специально выбранной системы координат своим уравнением x²/a²+y²/b²-z²/c²=1. Если точка с координатами (x, y, z) принадлежит однополостному гиперболоиду, то и точки (±x, ±y, ±z) при любом наборе + и - также принадлежат однополостному гиперболоиду, следовательно начало координат является центром симметрии однополостного гиперболоида, оси координат его главными осями, а координатные плоскости являются плоскостями симметрии — его главными плоскостями. Будем считать, что a≥b. Если a=b, то однополостный гиперболоид получается вращением гиперболы x²/a²-z²/c²=1 вокруг её мнимой оси (oz) и поверхность в этом случае называется однополостным гиперболоидом вращения. Вершинами однополостного гиперболоида называются точки пересечения поверхности с осями координат.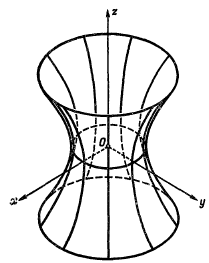

https://uchim.org/algebra-i-geometrija/odnopolostnyj-giperboloid - uchim.org

Замечание: однополостный гиперболоид может быть получен из равностороннего однополостного гиперболоида вращения X²+Y²-Z²=1 с помощью равномерных сжатий x=aX, y=bY, z=cZ.

Всё для учебы » Аналитическая геометрия » Однополостный гиперболоид