Эллипсоид
Эллипсоидом в специально выбранной прямоугольной системе координат называется поверхность, заданная уравнением x2/a2+y2/b2+z2/c2=1 (1). Если точка с координатами (x, y, z) лежит на эллипсоиде, то и точка (±x, ±y, ±z) при любом наборе знаков + и - лежит на этой поверхности. Значит начало координат (0, 0, 0) является центром симметрии эллипсоида, а координатные плоскости являются плоскостями симметрии.
Рассмотрим сечение эллипсоида плоскостью xoy. В результате сечения получается линия x2/a2+y2/b2=1, z=0, называемая эллипсом, центр которого расположен в начале координат, осями служит ось абсцисс и ось ординат. Аналогичным образом плоскости yoz (x=0) и xoz (y=0) пересекают эллипсоид по эллипсам. Рассмотренные сечения называют главными сечениями эллипсоида.
В уравнении эллипсоида (1) будем считать, что a≥b≥c. 1) Если a>b>c, то эллипсоид называется трехосным. 2) Если a>b=c, то эллипсоид называется вытянутым и получается вращением эллипса x2/a2+z2/c2=1 вокруг его большой оси. 3) Если a=b>c, то эллипсоид называется сжатым и получается вращением эллипса y2/b2+z2/c2=1 вокруг малой оси.
http://uchim.org/algebra-i-geometrija/jellipsoid - uchim.org
Рассмотрим сечение эллипсоида координатными плоскостями. 1) Сечение эллипсоида плоскостью xoy осуществляется по линии x2/a2+y2/b2+z2/c2=1, z=0, или x2/a2+y2/b2=1, z=0. Линия сечения в этом случае представляет собой эллипс с полуосями a и b, большая ось которого параллельна ox, малая - oy, а центр эллипса - начало системы координат xoy. 2) Сечение эллипсоида плоскостью xoz осуществляется по линии x2/a2+z2/c2=1, y=0. Данная линия представляет собой эллипс с полуосями a и b с центром в начале координат xoz. 3) Аналогичным образом сечение эллипсоида плоскостью yoz осуществляется по линии y2/b2+z2/c2=1, x=0, которая представляет собой эллипс с полуосями b и c с центром в начале координат системы yoz.Рассмотрим сечение эллипсоида произвольной плоскостью, параллельной одной из координатных плоскостей, например, плоскостью, параллельной xoy, которая определяется уравнением z=h, где h - любое вещественное число, плоскость z=h пересекает эллипсоид на линии, определяемой уравнениями x2/a2+y2/b2+h2/c2=1, z=h, или x2/a2+y2/b2=1-h2/c2, z=h.
а) |h|>c => 1-h2/c2<0. В таком случае первое уравнение неразрешимо ни при каких x, y. Значит плоскость z=h эллипсоид не пересекает.
б) |h|=с <=> h=±c. Если h=±c, то 1-h2/c2=0 => x2/a2+y2/b2=0, x=0, y=0. Значит плоскость встречает эллипсоид только в двух точках (0, 0, h) и (0, 0, -h).
в) Если |h|<c, то 1-h2/c2>0 => z=h пересекает эллипсоид по линии, определяемой уравнением:
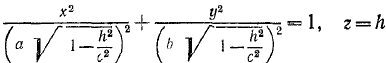, которая представляет собой эллипс с полуосями a'=a√(1-h2/c2) и b'=b√(1-h2/c2) с центром в O(0, 0, h). Из этих формул следует, что сечение эллипсоида плоскостью z=0 является наименьшим.Замечание: на практике эллипсоид может быть получен из сферы X2+Y2+Z2=1, полученной с помощью трех равномерных сжатий x=aX, y=bY, z=cZ, направленных перпендикулярно по отношению к плоскостям yoz, xoz, xoy соответственно.
Всё для учебы » Аналитическая геометрия » Эллипсоид