Пучок плоскостей
Собственным пучком плоскостей называется множество всех плоскостей, проходящих через одну прямую.
Несобственным пучком плоскостей называется множество всех параллельных между собой плоскостей.
Теорема 1. Для того чтобы три плоскости, заданные своими общими уравнениями A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0, A3x+B3y+C3z+D3=0 относительно ПДСК принадлежали одному пучку, собственному или несобственному, необходимо и достаточно, чтобы ранг матрицы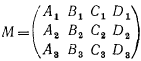 был равен или двум, или единице.
был равен или двум, или единице.
Теорема 2. Пусть относительно ПДСК заданы две плоскости π1 и π2 своими общими уравнениями: A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0. Для того чтобы плоскость π3, заданная относительно ПДСК своим общим уравнением A3x+B3y+C3z+D3=0, принадлежала пучку, образованному плоскостями π1 и π2, необходимо и достаточно, чтобы левая часть уравнения плоскости π3 представлялась как линейная комбинация левых частей уравнений плоскостей π1 и π2.
Несобственным пучком плоскостей называется множество всех параллельных между собой плоскостей.
Теорема 1. Для того чтобы три плоскости, заданные своими общими уравнениями A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0, A3x+B3y+C3z+D3=0 относительно ПДСК принадлежали одному пучку, собственному или несобственному, необходимо и достаточно, чтобы ранг матрицы
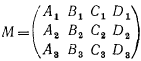 был равен или двум, или единице.
был равен или двум, или единице.Теорема 2. Пусть относительно ПДСК заданы две плоскости π1 и π2 своими общими уравнениями: A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0. Для того чтобы плоскость π3, заданная относительно ПДСК своим общим уравнением A3x+B3y+C3z+D3=0, принадлежала пучку, образованному плоскостями π1 и π2, необходимо и достаточно, чтобы левая часть уравнения плоскости π3 представлялась как линейная комбинация левых частей уравнений плоскостей π1 и π2.
Доказательство необходимого условия. Дано: плоскость π3 принадлежит пучку, образованному плоскостями π1 и π2, следовательно, π1, π2, π3 принадлежат одному пучку плоскостей. Так как плоскости π1 и π2 различны, то ранг матрицы M≤2. Следовательно, левые части уравнения плоскостей π1 и π2 линейно независимы. Поэтому, левая часть в уравнении плоскости π3 может быть представлена как линейная комбинация плоскостей π1 и π2, то есть существуют константы λ и μ, такие, что (1) A3x+B3y+C3z+D3=λ(A1x+B1y+C1z+D1)+μ(A2x+B2y+C2z+D2), где A3=λA1+μA2, B3=λB1+μB2, C3=λC1+μC2, D3=λD1+μD2.
https://uchim.org/algebra-i-geometrija/puchok-ploskostej - uchim.org
Докажем достаточные условия теоремы 2. Дано: равенство 1, требуется доказать, что π1, π2, π3 принадлежат одному пучку плоскостей. В самом деле, из равенства 1 следует, что A3=λA1+μA2, B3=λB1+μB2, C3=λC1+μC2, D3=λD1+μD2. Тогда третья строка матрицы M есть линейная комбинация первых двух строк этой матрицы. Следовательно, ранг матрицы M≤2, тогда, в силу теоремы 1, плоскость π3 принадлежит пучку плоскостей, образованному π1 и π2. Следствие из теоремы 2: уравнение плоскости, проходящей через прямую пересечения двух плоскостей π1 и π2, заданных своими общими уравнениями относительно ПДСК, имеет вид A1x+B1y+C1z+D1+α(A2x+B2y+C2z+D2)=0, α=μ/λ≠0.Всё для учебы » Аналитическая геометрия » Пучок плоскостей