Гиперболический параболоид

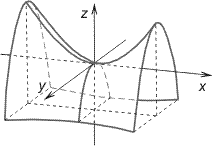
Гиперболическим параболоидом называется поверхность второго порядка, заданная относительно специально выбранной прямоугольной системы координат уравнением: x²/p-y²/q=2z, p, q>0, p≥q (1).

https://uchim.org/algebra-i-geometrija/giperbolicheskij-paraboloid - uchim.org

Если точка с координатами (x, y, z) лежит на гиперболическом параболоиде, то точки с координатами (±x, ±y, ±z) при любом наборе знаков также лежат на этой поверхности. Следовательно, плоскости xoy и yoz являются плоскостями симметрии гиперболического параболоида, а сечения, образованные данными плоскостями с поверхностью называются главными сечениями. Ось oz является осью симметрии гиперболического параболоида, если p≠q. Если p=q, то гиперболический параболоид имеет еще две оси симметрии, заданные уравнениями y=x, z=0 и y=-x, z=0. Вершиной гиперболического параболоида называется пересечение поверхности с oz. В данном случае вершиной поверхности является точка O(0, 0, 0).

Всё для учебы » Аналитическая геометрия » Гиперболический параболоид